Cómo confirmar la exactitud dimensional de una bola de precisión

Las bolas están presentes en rodamientos tanto para aplicaciones de movimiento lineal como rotatorio en máquinas-herramienta, actúan como contactos y puntos de pivote en equipos de medición y herramientas, pueden actuar como émbolos en bombas hidráulicas y sirven como patrones para la medición de tamaño y redondez. También son útiles para verificar el paralelismo de superficies en medidores con yunques planos y contactos sensibles, incluidos muchos medidores de espesor o de presión.

El usuario toma medidas con la bola en cada esquina de un yunque cuadrado o en las posiciones de las 3 y las 9 en punto y las posiciones de las 6 y 12 en punto de un yunque redondo. Conociendo estas lecturas, el usuario ajusta el yunque en consecuencia para llevar todos los puntos dentro de la tolerancia de paralelismo.

Independientemente de si se utiliza una bola en un ensamblaje, como herramienta o como patrón para fines de inspección, primero es necesario confirmar su precisión dimensional. Como ocurre con la mayoría de los estándares dimensionales, la exactitud de una bola de precisión debe ser aproximadamente 10 veces mayor que la resolución del medidor utilizado para la calibración, y el instrumento usado para medir la bola debe ser 10 veces más preciso que ellos. En consecuencia, una bola de precisión se mide comúnmente en micropulgadas, o incluso en fracciones de micropulgadas.

Creación de un alistamiento de medición preciso

Los medidores de comparación utilizados para medir bolas no solo deben medir en millonésimas, también deben medir hasta millonésimas y cumplir con los más altos estándares de estabilidad y precisión. Esto significa que el medidor debe ser robusto, con componentes de gran tamaño que se puedan bloquear entre sí para garantizar una rigidez extrema.

Dado que la bola es redonda, una buena práctica de medición requiere contactos planos para medir el diámetro de la bola. Esto requiere que los yunques sean extremadamente paralelos, y aunque se puede emplear un tope para colocar la bola en la misma ubicación, el paralelismo del yunque sigue siendo crítico. Para ayudar a asegurar el paralelismo, un yunque inferior especial en el medidor de bola permite el ajuste del paralelismo con el contacto superior sensible.

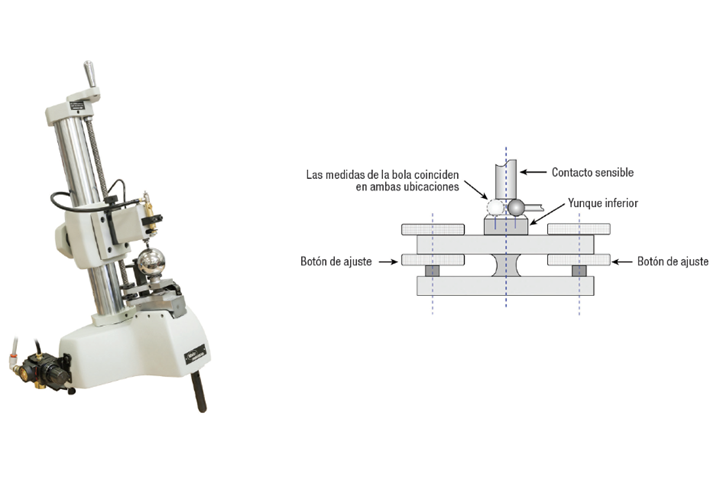
Es necesario un comparador robusto para obtener mediciones precisas. Este diagrama muestra una configuración común al medir bolas.

El uso de sondas de medición sin fricción debería asegurar una presión de medición constante, alto rendimiento y baja histéresis, lo que promueve una medición con precisión de millonésimas. Además, para asegurar un posicionamiento repetible de la bola, los usuarios deberían instalar una cama con muesca en V en el yunque para ubicar la bola. Finalmente, los usuarios deberían inclinar todo el medidor hacia atrás para que la gravedad asegure la bola entre la muesca y el yunque de referencia antes de que el usuario coloque en sitio el contacto sensible para la medición. Los usuarios necesitarán configurar y utilizar el medidor en un ambiente controlado, apropiado para mediciones de micropulgadas, además de tomar medidas de protección contra la contaminación y las influencias térmicas.

Hay dos escuelas de pensamiento sobre el alistamiento de la medición: una es forzar la bola entre los contactos para “limpiar” el polvo y el aceite que podrían sesgar la medición. Otra es retraer el contacto superior con una palanca de elevación antes de colocar la bola en el escenario para asegurar una presión constante entre las pruebas y reducir la tensión en el mecanismo. Si bien la investigación sobre la efectividad de cada una no es concluyente, la mayoría de los usuarios se inclinan hacia el método de retracción, colocando la sonda una vez que la bola está en su lugar. Esto reduce la tensión en el contacto sensible y proporciona un contacto de sonda repetible con la bola que está siendo medida.

Comprobación de la precisión

Después de preparar una configuración precisa, uno puede pensar que medir una bola es simple, pero hay más que un solo diámetro.

Cuando los usuarios especifican una bola, generalmente se enfocan en su diámetro nominal (D), es decir, el valor por el cual se identifica: piense en 0.5 pulgadas o 12 mm. Este diámetro debe estar dentro del rango de su tolerancia de fabricación y corresponder al diámetro único de la bola (Ds), que es la distancia entre dos planos paralelos tangentes a la superficie de la bola.

Sin embargo, ninguna bola es perfectamente redonda o idéntica a otra. Cuando se utilizan bolas como patrones de calibración, es importante establecer el nivel de incertidumbre. Para lograr esto, las bolas individuales se miden varias veces en ubicaciones aleatorias con el fin de encontrar los diámetros mínimo y máximo. La diferencia entre estos, conocida como variación del diámetro de la bola, se calcula simplemente como VDs = Ds max - Ds min.

La utilización de varios parámetros adicionales puede ayudar a los propósitos de control de calidad. Un parámetro es el diámetro medio de la bola (Dm), la media aritmética de los diámetros individuales más grande y más pequeño de una bola, que se calcula como Dm = (Ds max + Ds min) / 2. Para tener en cuenta la variación de producción entre unidades, los fabricantes suelen medir en lotes. Los tamaños de lote suelen constar de 10 bolas, pero en algunos casos pueden ser de 50 o más. Los cálculos del diámetro medio del lote (DmL) y la variación del diámetro del lote (VDL) se basan en los diámetros medios de las bolas más grandes y más pequeñas del lote, de la siguiente manera:

   DmL = (Dm max + Dm min)/2

   VDL = Dm max - Dm min

Todas las anteriores son mediciones estáticas que los usuarios pueden realizar mediante un equipo de medición de comparación sencillo. Los fabricantes de rodamientos, sin embargo, necesitan más datos para predecir el rendimiento en condiciones dinámicas.

Estas mediciones adicionales se pueden realizar con medidores de geometría circular (redondez), que pueden generar círculos de mínimos cuadrados, analizar la geometría de ondulación en una forma proporcional a la velocidad y realizar análisis armónicos para predecir los efectos de ruido de la geometría de la pieza a varias velocidades y bajo diferentes cargas.

Para los talleres de máquinas que utilizan bolas, principalmente, como estándares de medición, los medidores de comparación precisos pueden proporcionar todos los datos necesarios para garantizar la precisión.